I hear a lot about one-tailed test and two-tailed test. I don’t know what they are and how to apply them. Any advice will be appreciated.

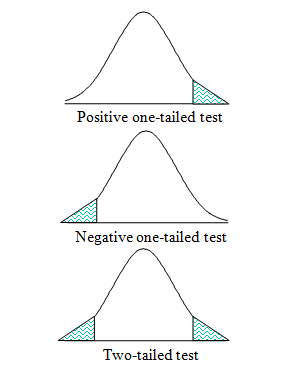
One-tailed test applies in situation where the researcher knows the direction the results should point. For example, when testing a new drug against a placebo, a researcher would want to know whether the new drug is better than the placebo. On a family of normal distribution curves a one-tailed test can be in one direction only, positive or negative (see diagram).

Two-tailed test applies in situation where the researcher does not know or is interested in both directions of the results. The two-tailed test is more commonly use than the one-tailed test. See diagram below for graphical representation.

You must decide before you collect your data whether you are doing a one-tailed or two-tailed test.

 What is an Independent-samples t test (two-sample t test) and when can it be used?

This is one specific example of a group of test in statistics know as t test. This is used to compare the means of one variable for two groups of cases.  As an example, a practical application would be to find out the effect of a new drug on blood pressure.  Patients with high blood pressure would be randomly assigned into two groups, a placebo (control) group and a treatment (experimental) group.  The placebo group would receive conventional treatment while the treatment group would receive a new drug that is expected to lower blood pressure.  After treatment for a couple of months, the two-sample t test is used to compare the average blood pressure of the two groups.  Note that each patient is measured once and belongs to one group. You use this test for normally distributed data and when the variances between the two groups are equal.

What is paired-samples t test (dependent t test) and when can it be used?

This is one specific example of a group of test in statistics know as t test. This is used to compare the means of two variables for a single group.  The procedure computes the differences between values of the two variables for each case and tests whether the average differs from zero.  For example, you may be interested to evaluate the effectiveness of a mnemonic method on memory recall.  Subjects are given a passage from a book to read, a few days later, they are asked to reproduce the passage and the number of words noted.  Subjects are then sent to a mnemonic training session.  They are then asked to read and reproduce the passage again and the number of words noted.  Thus each subject has two measures, often called before (pre) and after (post) measures.

An alternative design for which this test is used is a matched-pairs or case-control study.  To illustrate an example in this situation, consider treatment patients.  In a blood pressure study, patients and control might be matched by age, that is, a 64-year-old patient with a 64-year-old control group member.  Each record in the data file will contain responses from the patient and also for his matched control subject. You use this test for normally distributed data.

What is one-sample t test and when can it be used?

This is one specific example of a group of test in statistics know as t test. This is used to compare the mean of one variable with a known or hypothesised value.  In other words, the One-sample t tests procedure tests whether the mean of a single variable differs from a specified constant.  For instance, you might be interested to test whether the average IQ of some 50 students differs from an IQ of 125; or how the average salary in Newcastle compares to the national average.

I hear a lot about p-value. What is it and how do I interpret it?

The p stands for probability therefore the p-value is a probability value between zero and one. It helps you to draw conclusion about statistics you perform. The three common situations are:

1. If the p-value is greater than 0.05, the null hypothesis is accepted and the result is not significant.
2. If the p-value is less than 0.05 but greater than 0.01, the null hypothesis is rejected and the result is significant beyond the 5 percent level.
3. If the p-value is smaller than 0.01, the null hypothesis is rejected and the result is significant beyond the 1 percent level.

The null and alternative hypotheses are simply two opposing statements that you make concerning your research question.

How do I perform a normality test in SPSS?

Follow these steps to perform the normality test:

1. From the menu bar select Analyze -> Descriptives Statistics -> Explore….
2. Transfer a continuous variable e.g. blood pressure [bloodpres] to Dependent List:.
3. Transfer a grouping variable gender to Factor List:.
4. From Display click on Plots. Then click on Plots….
5. Under Descriptive deselect Stem-and –leaf.
6. Select Normality plots with tests.
7. Click on Continue. Click on OK.

Examine the result on the table Tests of Normality. For a small sample size (n≤50) use the Shapiro-Wilk statistic. For large sample size (n>50) use the Kolmogorov-Smirnov statistic. Note that p values (usually under the column Sig.) >0.05 means that your data is normally distributed.

How do I perform an homogeneity of variance test in SPSS?

Follow these steps to perform the homogeneity of variance test:

1. Select Analyze -> Compare Means -> One-Way ANOVA….
2. Transfer a continuous variable e.g. blood pressure [bloodpres] to Dependent List:.
3. Transfer a grouping variable gender to Factor List:.
4. Click on Options and select Homogeneity of variance test.
5. Click Continue and click OK.

Examine the table Test of Homogeneity of variance. Note that if the p value is >0.05 then the variances between the two groups are equal. Ignore the table ANOVA which is also produced as part of this procedure.

How do I perform an independent Samples T Tests in SPSS?

This test is suitable only for normally distributed data and when the variances between the two groups are equal. Follow these steps to perform the test:

1. Select Analyze -> Compare Means -> Independent-Samples T Test….
2. Transfer the continuous variable e.g. blood pressure to Test Variable(s):.
3. Transfer the grouping variable e.g. gender to Grouping Variable:.
4. Click on Define Groups. Beside Group 1: type 1. Beside Group 2: type 2.
5. Click on Continue and click on OK.

If you are not sure how to interpret the output recall the dialogue box via Analyze -> Compare Means -> Independent-Samples T Test…. Click on Help. Then click on Show me on the displayed window to go through a case study. The case study uses a different data file to explain every bit of the output.

My data is not normal. Which test should I use to find out if there are significant differences between groups?

You should use the Mann-Whitney U Test. Follow these steps:

1. Select Analyze -> Nonparametric Tests -> 2 Independent-Samples T Test….
2. Transfer the continuous variable e.g. blood pressure to Test Variable(s):.
3. Transfer the grouping variable e.g. gender to Grouping Variable:.
4. Click on Define Groups. Beside Group 1: type 1. Beside Group 2: type 2.
5. Click on Continue and click on OK.

How do I perform a paired samples t test (Dependent T Test) in SPSS?

This test is also suitable for normally distributed data. There is no need for homogeneity of variance test because we are dealing with the same group. To do the actual test, follow these steps:

1. From the menu bar select Analyze -> Compare Means -> Paired Samples T Test….
2. Click on variable1 and click on the arrow.
3. Click on variable2 and click on the arrow. Click OK.

If you are not sure how to interpret the output recall the dialogue box via Analyze -> Compare Means -> Paired -Samples T Test…. Click on Help. Then click on Show me on the displayed window to go through a case study. The case study uses a different data file to explain every bit of the output.

I have paired sample data that are not normally distributed. Which test should I use in SPSS?

You should use Wilcoxon Signed Ranks test. Follow these steps:

1. From the menu bar select Analyze -> Nonparametric Tests -> Paired Samples T Test….
2. Click on variable1 and click on the arrow.
3. Click on variable2 and click on the arrow. Click OK.

How do I perform a One-Sample T Test in SPSS?

To do the test, follow these steps:

1. From the menu bar select Analyze -> Compare Means -> One-Sample T Test….
2. Select the continuous variable e.g. Intelligence Quotient [iq] and click on the arrow.
3. Type a value e.g. 125 besides Test Value:.
4. Click OK.

If you are not sure how to interpret the output recall the dialogue box via Analyze -> Compare Means -> One -Samples T Test…. Click on Help. Then click on Show me on the displayed window to go through a case study. The case study uses a different data file to explain every bit of the output.

What is correlation?

A correlation is a statistic used for measuring the strength of a supposed linear association between two variables. The most common correlation coefficient is the Pearson correlation coefficient, use to measure the linear relationship between two interval variables that are normally distributed. Generally, the correlation coefficient varies from -1 to +1.  If your data is ordinal or not normally distributed you use the Spearman Rho. If you have two nominal variables and want to find the relationship (association) between them you will use Chi-Square.

How do I produce the Pearson or Spearman Rho correlation coefficient in SPSS?

To produce the correlation coefficient select:
Analyze -> Correlate -> Bivariate…

This will open the Bivariate Correlation dialog box. Transfer the two variables to the Variables text box.  Select the correlation you want by a single click on the dialog box.

Could you possibly tell me how to calculate the Intraclass correlation co-efficient in SPSS? I am aware of the file structure required, but I just cannot find the statistic in the analysis menu.

To find the Intraclass correlation coefficient (ICC), from SPSS menu bar select: Analyze -> Scale -> Reliability Analysis... Then click on the Statistics push button. You will then see ICC towards the bottom of the dialogue box. 

How to do Simple One-Way Analysis of variance (ANOVA) in SPSS?

First of all your data should be like this

1=group 1, 2=group 2 etc. Measure1, measure2 are your continuous variables. You can have more than 2.

1. Analyze -> Compare Means -> One-way ANOVA....
2. Transfer your variables e.g. measure1, measure2, to Dependent List:
3. Transfer group to Factor:
4. Click OK.

Note that you can click on Help on the Dialogue box to get more information and a case study. For the case study click on Show Me on the displayed window.

I have just done an ANOVA test in SPSS and the result was significant. Now I would like to pin-point the differences. How can I do this in SPSS?

You need to do a post-hoc test. To do this, recall the ANOVA dialogue box via Analyze -> Compare Means -> One-way ANOVA....Then click on Post-Hoc...and select the appropriate test e.g. Bonferroni or Tukey. Click on Continue and OK to generate the output.

Please give me a reference that says that the assumption of normality is not necessary for ANOVA.

SPSS 8.0 Guide to Data Analysis, p263. Marija J. Norusis, Prentice Hall, 1998.

Why is the cut off alpha level of 5% (0.05) used?

One colleague John David Sorkin M.D., Ph.D. answered this question nicely. And I quote him here

“We must remember that there is nothing "magical" about a p<0.05. There is no science behind the choice of 0.05 as indicating significance as compared to any other value. What is the difference between a p<0.04 which we say is significant and one that is <0.06 which we say is not significant? They both differ from the magical 0.05 by 0.01! The choice of 0.05 comes from R.A. Fisher who pulled the value out of the air. It is, I believe far better to give the effect size along with a measure of its precision (i.e. the Standard Error) and a p value, or perhaps better the effect and a 95% confidence interval around the effect without getting tied into knots determining what is statistically significant and what is not. It is all too easy to fall into the trap of saying that one will pay attention to a test associated with a p<0.05 (or <=0.05) and ignore results with any larger p value. We must also remember statistical significance does not mean a result is important, and conversely”.