Paired Samples T Test (Dependent Samples T test)
Paired-samples t test (dependent t test)
This is used to compare the means of two variables for a single group. The procedure computes the differences between values of the two variables for each case and tests whether the average differs from zero. For example, you may be interested to evaluate the effectiveness of a mnemonic method on memory recall. Subjects are given a passage from a book to read, a few days later, they are asked to reproduce the passage and the number of words noted. Subjects are then sent to a mnemonic training session. They are then asked to read and reproduce the passage again and the number of words noted. Thus each subject has two measures, often called before (or pre) and after (or post) measures.
An alternative design for which this test is used is a matched-pairs or case-control study. To illustrate an example in this situation, consider treatment patients. In a blood pressure study, patients and control might be matched by age, that is, a 64-year-old patient with a 64-year-old control group member. Each record in the data file will contain responses from the patient and also for his matched control subject.
Assumptions underlying the use of t test
Before we look at the details of how to perform and interpret a t test, it is good idea for you to understand the assumptions underlying the use of t test. The assumptions are:
- your data is normally distributed
- the variances between the groups are equal
- the sample size is adequate (at least 30 cases per group)
So, before you carry out any t test, you must check to make sure that your data satisfy all these assumptions. However, if your data seriously violates any of these assumptions then Non-parametric tests should be used. Non-parametric tests do not carry specific assumptions about population distributions, variance and sample size.
Exercise
Perform a Paired-samples t test (dependent t test) on the data on Table 1. This data file is stored in this location \\campus\software\dept\spss and is called b4_after training words.sav.
Table 1: Number of words recalled
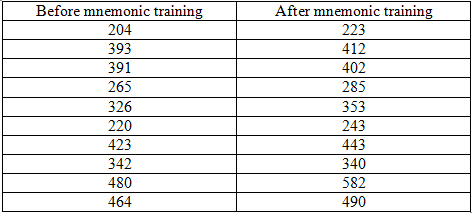
You need to check whether the number of words recalled before training and after training are normally distributed.
Why do you think in this case it not necessary to perform the homogeneity of variance test?
Write down the null and alternative hypotheses for the Paired-samples t test (dependent t test):
Null Hypothesis (Ho): There is no difference in the average number of words recalled before and after training.
Alternative Hypothesis (H1): There is a difference in the average number of words recalled before and after training.
Normality Test
Follow these steps to perform the normality test:
- From the menu bar select Analyze -> Descriptives Statistics -> Explore….
- Transfer number of words recalled before training [words_b4] to Dependent List:.
- Transfer number of words recalled after training [words_af] to Dependent List:.
- From Display click on Plots. Then click on Plots….
- Under Descriptive deselect Stem-and –leaf.
- Select Normality plots with tests.
- Click on Continue. Click on OK.
Examine the output. What would you conclude?
Paired Samples T Test (Dependent T Test)
Since number of words recalled before training [words_b4] was normally distributed and number of words recalled after training [words_af] was also normally distributed, we need to perform a parametric paired samples t test. There was not need to homogeneity of variance test because we are dealing with the same group. To do the actual test, follow these steps:
- From the menu bar select Analyze -> Compare Means -> Paired Samples T Test….
- Click on number of words recalled before training [words_b4] and click on the arrow.
- Click on number of words recalled after training [words_af] and click on the arrow. Click OK.
Use the output to answer these questions.
Using the table Paired Sample Statistics what is the average value of the number of words recalled before training [words_b4]? What is the average value of the number of words recalled after training [words_af]? Which of these two averages is more variable?
Using the table Paired Samples Test, what is the mean difference between the two averages? Is this difference significant? Why? Will you accept or reject the null hypothesis? Why?
