Theoretical modelling of Bose-Einstein condensates

Condor is used intensively by several research projects in this School

Stuart Cockburn writes

"Using laser cooling techniques, certain alkali gases can be made to undergo a phase transition to a novel state of matter called a Bose-Einstein condensate - the coldest matter currently known in the Universe. The field of ultracold Bose gases has undergone a tremendous period of expansion over the past fifteen years or so, since Bose-Einstein condensates were first produced within laboratories in 1995. The importance of this achievement was recognized by the Nobel prize committee, who awarded the 2001 Physics prize to Eric Cornell, Wolfgang Ketterle and Carl Wieman for the creation and early study of this type of matter.

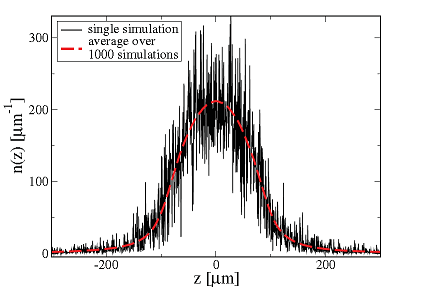
The research that we undertake at Newcastle aims to theoretically model Bose-Einstein condensates, focusing in particular on the effects of finite-temperature. The theory that we use for this task is called the Stochastic Gross-Pitaevskii equation (SGPE). This theory is difficult to solve analytically, so solutions require computational methods. A key feature of the the SGPE simulations is that we need to average over many repeated calculations to gain useful information (compare the noisy single run data to the more useful, smoother average data shown in the figure attached). The Condor system dramatically speeds up the computation process for us, as it allows many of these simulations to run in parallel, rather than running as serial jobs on a single computer.

A typical SGPE data set might be made up of 1000 single simulations, each of which could individually take between an hour and a number of days to complete. Processing these jobs in parallel reduces this time greatly, by a factor equal to the number of free machines on the Condor grid, which is usually around several hundred. Consider the specific case where a single simulation takes 1 day to complete, then 1000 such jobs would take almost three years to finish if performed one after another. However, if there are 200 machines available via Condor, this reduces the simulation time from a few years to a few days. As such, Condor represents a valuable tool which plays an integral role in the research that we currently carry out."

Condor has contributed to the following papers:

• Fluctuating and dissipative dynamics of dark solitons in quasi-condensates S.P. Cockburn, H.E. Nistazakis, T.P. Horikis, P.G. Kevrekidis, N.P. Proukakis, D.J. FrantzeskakisarXiv:1107.3855 (submitted to Physical Review A)
• Quantitative study of quasi-one-dimensional Bose gas experiments via the stochastic Gross-Pitaevskii equation S. P. Cockburn, D. Gallucci, and N. P. Proukakis Phys. Rev. A 84, 023613 (2011) – Published August 8, 2011
• Comparison between microscopic methods for finite-temperature Bose gases S. P. Cockburn, A. Negretti, N. P. Proukakis, and C. Henkel Phys. Rev. A 83, 043619 (2011) – Published April 21, 2011
• Matter-Wave Dark Solitons: Stochastic versus Analytical Results S. P. Cockburn, H. E. Nistazakis, T. P. Horikis, P. G. Kevrekidis, N. P. Proukakis, and D. J. Frantzeskakis Phys. Rev. Lett. 104, 174101 (2010) – Published April 29, 2010
• Stochastic Gross-Pitaevskii equation and some Applications S. P. Cockburn and N. P. Proukakis Laser Physics, 2009, Vol. 19, No. 4 (Special Issue on Physics of Cold Trapped Atoms)