Analysis of Variance (ANOVA)
Analysis of Variance (ANOVA)
Simple One-Way Analysis of Variance (ANOVA)
ANOVA is concerned with the testing of hypotheses about means. It is very similar to t-test. In fact, for an experiment involving two groups, output from ANOVA and t-test will be the same. However, t-test cannot be used to test hypothesis on three or more groups. So, if there are just two groups use t-test. If there are three groups or more use ANOVA.
Assumptions
- your data is normally distributed
- the variances between the groups are equal
- the sample size is adequate (at least 30 cases per group)
Before performing the ANOVA test you must check to ensure that your data satisfies the first two assumptions. The last assumption is only important if you want to extrapolate the findings from your sample to the population from which the sample was drawn from.
Preparing the Data
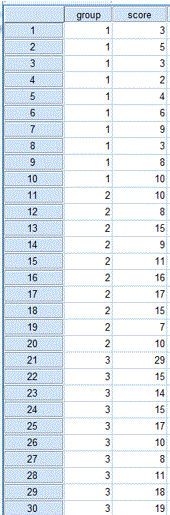
The data file for this example is shown on the table below. Create an SPSS data file using the table. The variables (corresponding to columns in the data file) are:
- group (1=control group, 2=mnemonic A group and 3=mnemonic B group)
- score number of words recalled
ANOVA Table 1
Students were put into 3 groups, control, group A and group B. Students in the control group received no training, while students in group A received a mnemonic training method and students in group B received a different mnemonic training method. After the training, the students were assessed and given a score. Has mnemonic training made any difference to the students’ performance measured using score? Which mnemonic training method is better?
Carry out a simple one-way ANOVA test on the data set using the variable score as dependent list and group as factor. Note you have to test the assumptions mentioned above before you proceed. This will help you decide whether you perform a parametric or nonparametric ANOVA.
Normality Test
Follow these steps to perform the normality test:
- From the menu bar select Analyze -> Descriptives Statistics -> Explore….
- Transfer score [number of words recalled] to Dependent List:.
- Transfer Group Membership [group] to Factor List:.
- From Display click on Plots. Then click on Plots….
- Under Descriptive deselect Stem-and –leaf.
- Select Normality plots with tests.
- Click on Continue. Click on OK.
The completed dialogue box is shown below:
ANOVA Fig 1
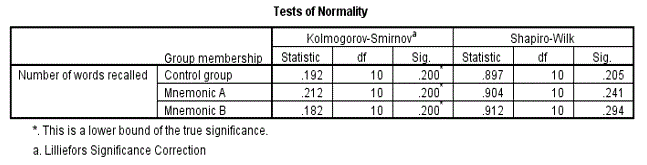
Examine the result on the table Tests of Normality (shown below). For a small sample size (n≤50) use the Shapiro-Wilk statistic. For large sample size (n>50) use the Kolmogorov-Smirnov statistic. Note that the numbers in the column df represent the sample size.
ANOVA Fig 2
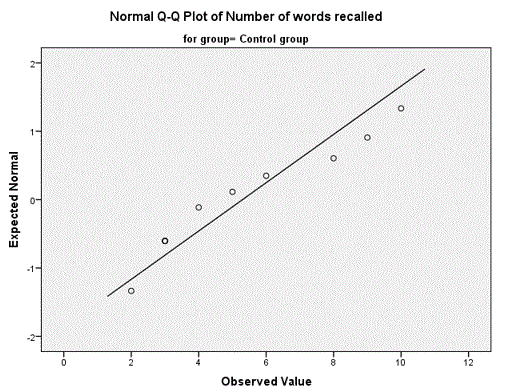
The table shows that score (number of words recalled) is normally distributed for all three groups [control group p=0.205 (>0.05); Mnemonic A group p=0.241 (>0.05) and Mnemonic A group p=0.294 (>0.05)]. The p values are all greater than 0.05 indicating that the distribution of score for the three groups is not significantly different from that of a normal distribution. Also look at the normal Q-Q plot to confirm the normality. Only the Q-Q plot for the control group is shown below.
ANOVA Fig 3
Homogeneity of variance test
Follow these steps to perform the homogeneity of variance test:
- Select Analyze -> Compare Means -> One-Way ANOVA….
- Transfer score [number of words recalled] to Dependent List:.
- Transfer Group Membership [group] to Factor.
- Click on Options and select Homogeneity of variance test.
- Click Continue and click OK.
Examine the table Test of Homogeneity of variance (shown below). What would you conclude? Ignore the ANOVA table for now which is also produced as part of this procedure.
ANOVA Fig 4
The results indicates that the variances of the 3 groups are equal [Levene Statistic=1.186, p=0.321 (>0.05)].
Running the ANOVA Procedure
Since the data satisfied the two assumptions, that is, score was normally distributed and the variances between the three groups are equal, we have to perform a parametric One-Way ANOVA.
From the menu bar:
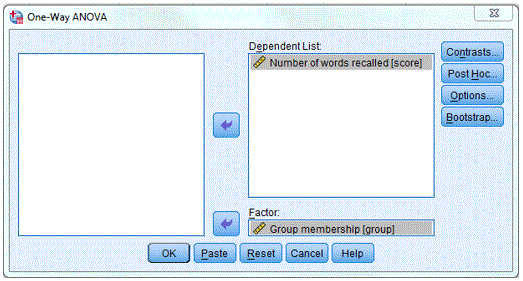
- Select Analyze -> Compare Means -> One-Way ANOVA….
- Click on Reset.
- Transfer score [number of words recalled] to Dependent List:.
- Transfer Group Membership [group] to Factor.
- Click on Options and select Descriptive. Deselect Homogeneity of variance test if it still selected.
- Click Continue and click OK.
The completed dialogue box is shown below.
ANOVA Fig 5
Examine the output. Two tables are produced.
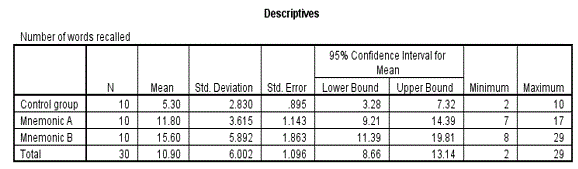
Descriptives Table
This table shows the summary statistics for the 3 groups, the mean scores are 5.30, 11.80 and 15.60 for control group, mnemonic A group and mnemonic B group respectively. Students from the control groups have the smallest mean compared to the other groups who received some sort of training. Are the means significantly different? The ANOVA table helps us to answer this question.
ANOVA Fig 6
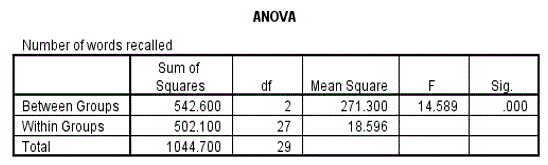
ANOVA Table
The table shows that there is a significant difference somewhere in the 3 means [F=14.589, p=0.001 (<0.05)]. Note that for very small p value, SPSS display it as .000. It is acceptable to approximate it to 0.001.
ANOVA Fig 7
Note that ANOVA can only tell us if there is a difference between the three groups or not. It does not justify us saying that any particular pairwise comparison is significant or not. In other words, in cases where there is significance, ANOVA does not tell us where the significance lies.
Post-hoc test
A planned comparison of means is known as a priori comparisons and unplanned is known as post-hoc comparisons. SPSS provide many post-hoc comparison tests; the most common are Tukey’s Honestly Significant Difference (HSD) and Scheffe’s test. After performing an ANOVA, to find where the differences lies between the groups, you need to carry out a post-hoc test. If the result from the ANOVA is not significant, there will be no need to perform a post-hoc test.
As the ANOVA table shows significance follow these instructions:
- Recall the ANOVA dialogue via Analyze -> Compare Means -> One-Way ANOVA….
- Click on Post-hoc and select Tukey and click on Continue.
- Click on OK.
Examine the output. The Descriptives and ANOVA tables are generated again; but we are now interested only in the Multiple Comparisons and Homogeneous Subsets tables.
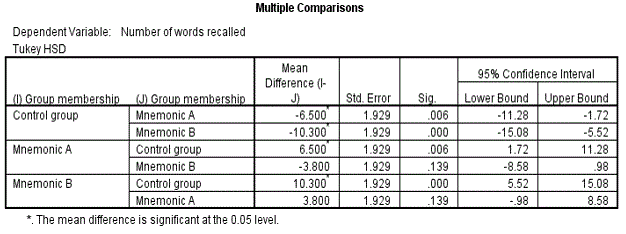
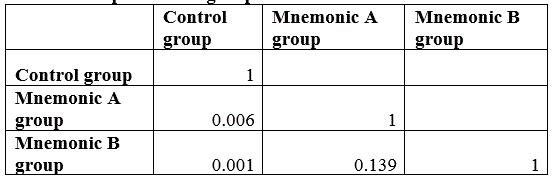
Multiple Comparisons Table
The table shows all the possible pairwise comparisons for the three groups and the associated p values.
ANOVA Fig 8
For example for the control group v mnemonic A group [mean difference=-6.50, p=0.006 (<0.05)]; this indicates that there a significant difference at the 5% level between the mean of the control group (mean=5.30) compared to the mean of mnemonic A group (mean=11.80). Similarly for the control group v mnemonic B group [mean difference=-10.30, p=0.001 (<0.05)]. Finally for the mnemonic A group v mnemonic B group [mean difference=-10.30, p=0.139 (>0.05)]; indicating that there is no significant difference between the means of the students who received training.
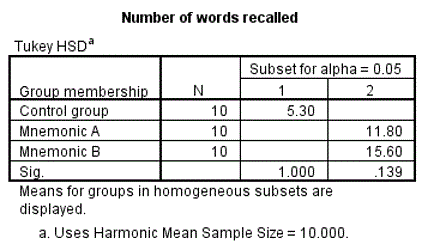
Homogeneous Subsets Table
The Homogeneous subsets tables shows which groups have same mean and which one have different mean. Notice that the control group is in subset 1 and mnemonic A and B groups are in subset 2. Within a subset there is no significance different while between subsets there is a significant difference. There is no significant difference between mnemonic A and mnemonic B groups while both these groups are significantly different from the control group as mentioned already.
ANOVA Fig 9
How to report ANOVA analysis (Summary)
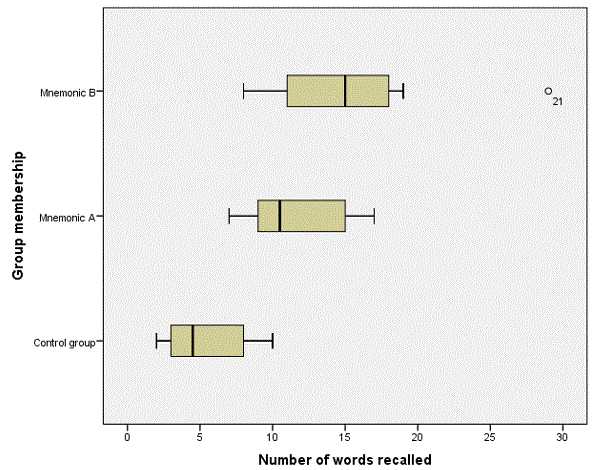
Normality and Homogeneity of variances test indicates that the data satisfied the assumptions for ANOVA test. ANOVA test shows that there was significant difference amongst the 3 groups [F=14.589, p=0.001 (<0.05)]. Post-hoc test further pin-point exactly where the differences was located; control group with a mean of 5.30 was significantly different from the mean of 11.80 for mnemonic A group [p=0.006 (<0.05)]. Similarly there was significant different for the control group v mnemonic B group [means of 5.30 v 15.60 respectively, p=0.001 (<0.05)]. Finally for the mnemonic A group v mnemonic B group [means 11.80 v 15.60, p=0.139 (>0.05)] there was no significant difference between the means of the students who received training. Students who received some sort of training did better than student who received no training, therefore mnemonic training has an effect on students’ performance. There was however no significance difference between the two mnemonic training methods. The table and box plot shows a summary of the results.
P Values of Pairwise Comparisons of groups
ANOVA Fig 10
ANOVA Fig 11
Non-parametric equivalent to ANOVA
Often data do not follow normal distribution or the variances between groups are not the same, when this happens you need to perform a Non-parametric equivalent to ANOVA.
Analyze -> Nonparametric Tests ->Legacy Dialogs -> K Independent Samples.