How to Perform and Interpret Factor Analysis Using SPSS

Introduction

Factor analysis is used to find latent variables or factors among observed variables. In other words, if your data contains many variables, you can use factor analysis to reduce the number of variables. Factor analysis groups variables with similar characteristics together. With factor analysis you can produce a small number of factors from a large number of variables which is capable of explaining the observed variance in the larger number of variables. The reduced factors can also be used for further analysis.

There are three stages in factor analysis:

1. First, a correlation matrix is generated for all the variables. A correlation matrix is a rectangular array of the correlation coefficients of the variables with each other.
2. Second, factors are extracted from the correlation matrix based on the correlation coefficients of the variables.
3. Third, the factors are rotated in order to maximize the relationship between the variables and some of the factors.

Example

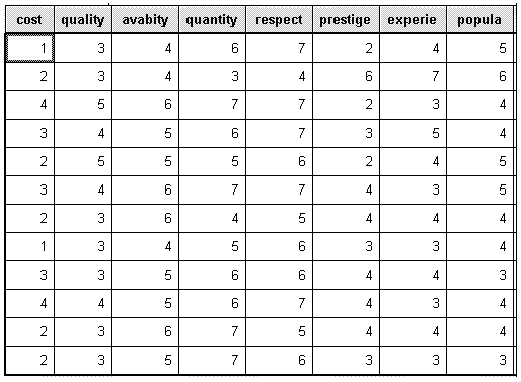
You may be interested to investigate the reasons why customers buy a product such as a particular brand of soft drink (e.g. coca cola). Several variables were identified which influence customer to buy coca cola. Some of the variables identified as being influential include cost of product, quality of product, availability of product, quantity of product, respectability of product, prestige attached to product, experience with product, and popularity of product. From this, you designed a questionnaire to solicit customers' view on a seven point scale, where 1 = not important and 7 = very important. The results from your questionnaire are show on the table below. Only the first twelve respondents (cases) are used in this example.

Table 1: Customer survey

Preparing the Data set

Prepare and enter the data into SPSS Data Editor window. If you do not know how to create SPSS data set see Getting Started with SPSS for Windows. Define the eight variables cost, quality, avabity, quantity, respect, prestige, experie, popula, and use the Variable Labels procedure to provide fuller labels cost of product, quality of product, availability of product, respectability of product, and so on to the variables names. The completed data set look like the one shown above in Table 1.

Running the Factor Analysis Procedure

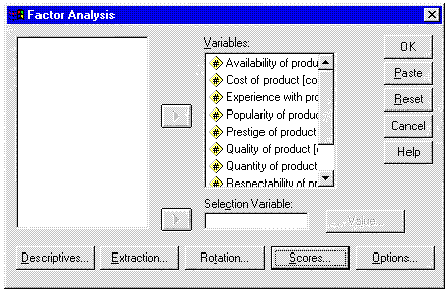
From the menu bar select Statistics and choose Data Reduction and then click on Factor. The Factor Analysis dialogue box will be loaded on the screen. Click on the first variables on the list and drag down to highlight all the variables. Click on the arrow (>) to transfer them to the Variables box. The completed dialogue box should look like the one shown below.

The Factor Analysis dialogue box

All we need to do now is to select some options and run the procedure.

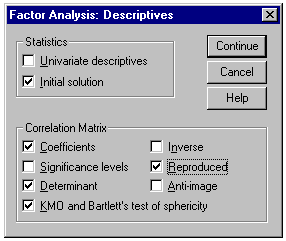
Click on the Descriptives button and its dialogue box will be loaded on the screen. Within this dialogue box select the following check boxes Coefficients, Determinant, KMO and Bartlett's test of sphericity, and Reproduced. Click on Continue to return to the Factor Analysis dialogue box. The Factor Analysis: Descriptives dialogue box should be completed as shown below.

The Factor Analysis: Descriptives dialogue box

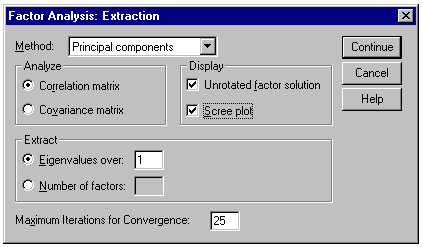
From the Factor Analysis dialogue box click on the Extraction button and its dialogue box will be loaded on the screen. Select the check box for Scree Plot. Click on Continue to return to the Factor Analysis dialogue box. The Factor Analysis: Extraction dialogue box should be completed as shown below.

The Factor Analysis: Extraction dialogue box

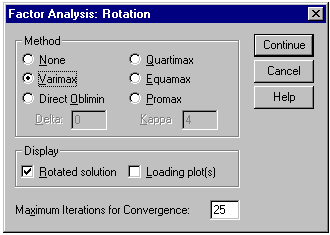
From the Factor Analysis dialogue box click on the Rotation button and its dialogue box will be loaded on the screen. Click on the radio button next to Varimax to select it. Click on Continue to return to the Factor Analysis dialogue box. The Factor Analysis: Rotation dialogue box should be completed as shown below.

The Factor Analysis: Rotation dialogue box

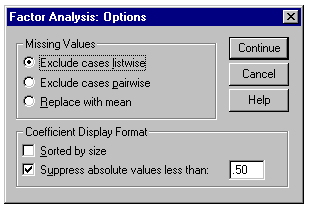
From the Factor Analysis dialogue box click on the Options button and its dialogue box will be loaded on the screen. Click on the check box of Suppress absolute values less than to select it. Type 0.50 in the text box. Click on Continue to return to the Factor Analysis dialogue box. Click on OK to run the procedure. The Factor Analysis: Options dialogue box should be completed as shown below.

The Factor Analysis: Options dialogue box

Interpretation of the Output

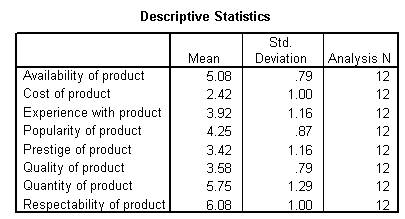
Descriptive Statistics

The first output from the analysis is a table of descriptive statistics for all the variables under investigation. Typically, the mean, standard deviation and number of respondents (N) who participated in the survey are given. Looking at the mean, one can conclude that respectability of product is the most important variable that influences customers to buy the product. It has the highest mean of 6.08.

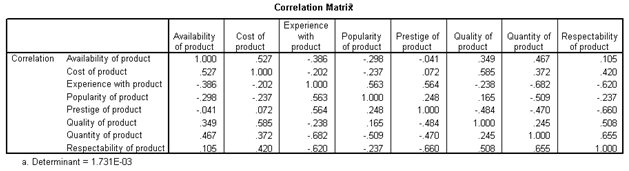
The Correlation matrix

The next output from the analysis is the correlation coefficient. A correlation matrix is simply a rectangular array of numbers which gives the correlation coefficients between a single variable and every other variables in the investigation. The correlation coefficient between a variable and itself is always 1, hence the principal diagonal of the correlation matrix contains 1s. The correlation coefficients above and below the principal diagonal are the same. The determinant of the correlation matrix is shown at the foot of the table below.

Kaiser-Meyer-Olkin (KMO) and Bartlett's Test

The next item from the output is the Kaiser-Meyer-Olkin (KMO) and Bartlett's test. The KMO measures the sampling adequacy which should be greater than 0.5 for a satisfactory factor analysis to proceed. Looking at the table below, the KMO measure is 0.417. From the same table, we can see that the Bartlett's test of sphericity is significant. That is, its associated probability is less than 0.05. In fact, it is actually 0.012. This means that the correlation matrix is not an identity matrix.

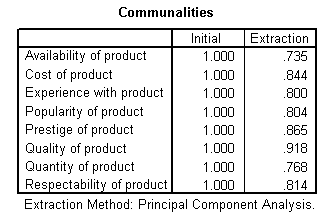
Communalities

The next item from the output is a table of communalities which shows how much of the variance in the variables has been accounted for by the extracted factors. For instance over 90% of the variance in quality of product is accounted for while 73.5% of the variance in availability of product is accounted for.

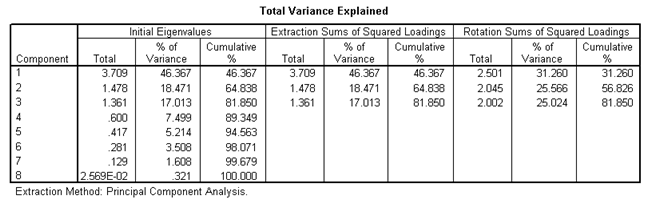
Total Variance Explained

The next item shows all the factors extractable from the analysis along with their eigenvalues, the percent of variance attributable to each factor, and the cumulative variance of the factor and the previous factors. Notice that the first factor accounts for 46.367% of the variance, the second 18.471% and the third 17.013%. All the remaining factors are not significant.

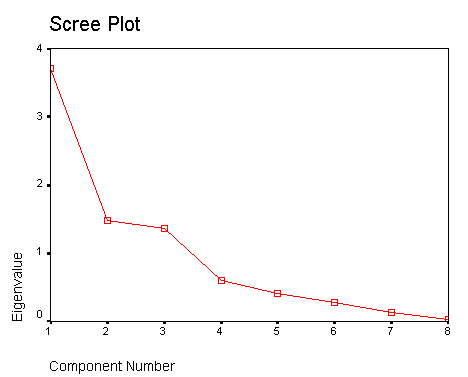
Scree Plot

The scree plot is a graph of the eigenvalues against all the factors. The graph is useful for determining how many factors to retain. The point of interest is where the curve starts to flatten. It can be seen that the curve begins to flatten between factors 3 and 4. Note also that factor 4 has an eigenvalue of less than 1, so only three factors have been retained.

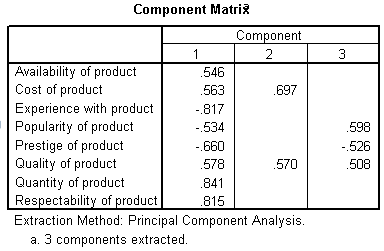
Component (Factor) Matrix

The table below shows the loadings of the eight variables on the three factors extracted. The higher the absolute value of the loading, the more the factor contributes to the variable. The gap on the table represent loadings that are less than 0.5, this makes reading the table easier. We suppressed all loadings less than 0.5.

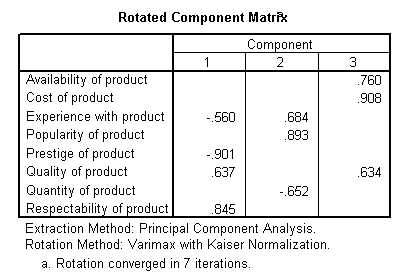
Rotated Component (Factor) Matrix

The idea of rotation is to reduce the number factors on which the variables under investigation have high loadings. Rotation does not actually change anything but makes the interpretation of the analysis easier. Looking at the table below, we can see that availability of product, and cost of product are substantially loaded on Factor (Component) 3 while experience with product, popularity of product, and quantity of product are substantially loaded on Factor 2. All the remaining variables are substantially loaded on Factor 1. These factors can be used as variables for further analysis.

Conclusion

You should now be able to perform a factor analysis and interpret the output. Many other items are produce in the output, for the purpose of this illustration they have been ignored. Note that the correlation matrix can be used as input to factor analysis. In this case you have to use SPSS command syntax which is outside the scope of this document.